-
- Üyelik Tarihi
- 3 Nis 2008
-
- Mesajlar
- 2,499
-
- MFC Puanı
- 0
Gamma Dağılımı Nedir - Gamma Dağılımı Hakkında - Matematikte Gamma Dağılımı
Olasılık kuramı ve istatistik bilim dallarında gamma dağılımı iki parametreli bir sürekli olasılık dağılımıdir. Bu parametrelerden biri ölçek parametresi θ; diğeri ise şekil parametresi k olarak anılır. Eğer k tamsayı ise, gamma dağılımı k tane üstel dağılım gösteren rassal değişkenlerin toplamını temsil eder; rassal değişkenlerin her biri nin üstel dağılımı için parametre
 olur.
olur.
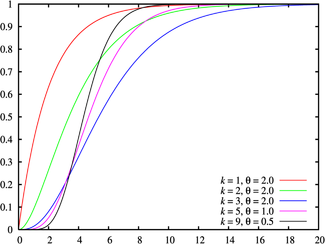
Yığmalı dağılım fonksiyonu
Karakteristikler
Bir rassal değişken olan Xin θ ölçek parametresi ve k şekil parametresi ile tanımlanmış bir gamma dağılımı ile ifade edilmesi için şu notasyon kullanılır:
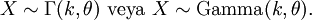
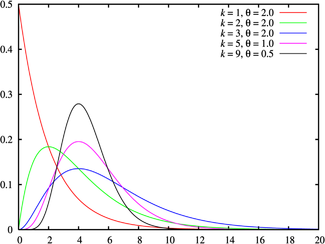
Olasılık yoğunluk fonksiyonu
Gamma dağılımının olasılık yoğunluk fonksiyonu şu şekilde bir gamma fonksiyonu ile ifade edilebilir:
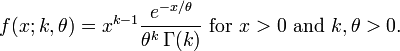
Bu çesit parametrelerle ifade edilme yukarıda verilen bilgi kutusunda ve grafiklerde kullanılmıştır.
Alternatif bir şekilde, gamma dağılımının olasılık yoğunluk fonksiyonu bir şekil parametresi α = k ile ölcek parametresinin tersi olan oran parametresi β = 1 / θ kullanılarak şöyle elde edilir:

Eger α bir pozitif tamsayı ise, o halde
Γ(α) = (α − 1)!
Olasılık yoğunluk fonksiyonu her iki şekli de istatistikçiler tarafından yaygın olarak kullanılmaktadır.
Yığmalı dağılım fonksiyonu
Yığmalı dağılım fonksiyonu bir tanzim edilmiş gamma fonksiyonudur ve bir tamamlanmamış gamma fonksiyonu şeklinde şöyle ifade edilir:

Özellikler
Toplama
Eğer i = 1, 2, ..., N için rassal değişken Xiin dağılımı bir Γ(αi, β) olursa; o halde

Ancak bütün Γ(αi, β) istatistiksel bağımsız olması gerekir.
Gamma dağılımı sonsuz bölünebilirlik özelliği gösterir.
Ölçekleme
Herhangi bir t için tX bir Γ(k, tθ) dağılımı goösterir; bu ifade θnın bir ölçek parametresi olduğunu gösterir.
Üstel ailesi
Gamma dağılımı iki-parametreli üstel ailesinin bir üyesidir ve doğal parametreler değerleri k − 1 ve − 1 / θ; ve doğal istatistikleri X ve ln(X) olur.
Enformasyon entropisi
Enformasyon entropisi şöyle verilir:

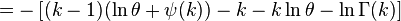

burada ψ(k) bir digama fonksiyonu olur.
KullbackLeibler ayrılımı
'Gerçek' dağılım olan Γ(α0, β0) ile yaklaşık fonksiyon olan Γ(α, β) arasındaki yönlendirilmiş Kullback-Leibler ayrılması şu fonksiyonla verilir:

Laplace dönüşümü
Gamma dağılımının Laplace dönüşümü şudur:

Parametre tahmini
Maksimum olabilirlilik tahmini
Birbirlerinden bagimsiz ve ayni dagilim gosteren N sayida gozlem , ,
 , icin olabilirlik fonksiyonu sudur:
, icin olabilirlik fonksiyonu sudur:

Bundan bir log-olabilirlilik fonksiyonu turetilebiliriz:

Bunun θ'ya gore maksimim degerini bulmak icin bu log-olabilirlilik fonksiyonunun birinci turevini alip sifira esitlersek, θ parametresi icin maksimum-olabilirlilik kestirimini buluruz:
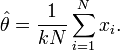
BUnu tekrara log-degisebilirlilik fonksiyonuna koyarsak, elde edilen ifade su olur:

Bunu k'ye gore maksimumunu bulmak icin birinci turevini aliriz ve bunu sifira esitleriz. Sonus sudur:

Burada
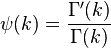
olup bir digamam fonksiyonudur.
k icin kapali-sekilli bir cozum bulunmamaktadir. Bu fonksiyon numerik olarak, hesaplamaya uygun davranis gosterir ve bunun icin bir numerik cozum istenirse, ornegin numerik Newton Yontemi, sonuclar yeterli dakik olur. Bu numerik cozumler icin ilk deger ya "momentler metodu" kullanilarak bulunur ya da su yaklasim kullanilabilir:

Eger su ifadeyi kullanirsak

k yaklasik su degerdedir:

Bu genellikle gercek degerden +/- %1,5 hatali olabilecegi bulunmustur. Bu ilk tahminin Newton-Raphson yontemi icin iyilestirilmesi Choi ve Wette (1969) soyle verilmistir:
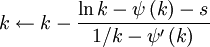
burada
 trigamma fonksiyonunu (yani digamma fonksiyonunun birinci turevini) ifade eder.
trigamma fonksiyonunu (yani digamma fonksiyonunun birinci turevini) ifade eder.
Digamma ve trigamma fonksiyonlarini cok dakiklikle hesaplamak guc olabilir. Fakat, su verilen yaklasim formulleri kullanarak birkaca onemli ondalikli sayiya kadar iyi yaklasim sayilarai bulmak imkani vardir:

ve

Ayrintilar icin bakiniz Choi ve Wette (1969).
Bayes tipi minimum ortalama-kareli hata
Bilinen degerde k ve bilinmeyen degerde 'θ, icin theta icin sonrasal olasilik yogunluk fonksiyonu (θ icin standard olcek-degeistilmez oncel kullanarak) su elde edilir:

Su ifade verilsin

Bunun θ entegrasyonu degiskenlerin degistirilmesi yontemi kullanilarak mumkun olur. Bunun sonucunda 1/θ ifadesinin

parametreleri olan bir gamma dagilimi gosterdigi ortaya cikartilir.
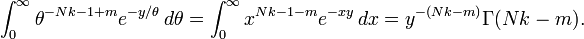
Momentler (m ile m = 0) orantisi alinarak hesaplanabilir:
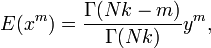
Buna gore theta'nin sonsal dagiligiminin ortalama +/- standart sapma kestiriminin soyle olur:

Gamma dağılım gösteren rassal değişken üretimi
İlişkili dağılımlar
Özel dağılımlar

Olasılık kuramı ve istatistik bilim dallarında gamma dağılımı iki parametreli bir sürekli olasılık dağılımıdir. Bu parametrelerden biri ölçek parametresi θ; diğeri ise şekil parametresi k olarak anılır. Eğer k tamsayı ise, gamma dağılımı k tane üstel dağılım gösteren rassal değişkenlerin toplamını temsil eder; rassal değişkenlerin her biri nin üstel dağılımı için parametre


Yığmalı dağılım fonksiyonu

Karakteristikler
Bir rassal değişken olan Xin θ ölçek parametresi ve k şekil parametresi ile tanımlanmış bir gamma dağılımı ile ifade edilmesi için şu notasyon kullanılır:
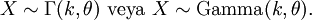
Olasılık yoğunluk fonksiyonu
Gamma dağılımının olasılık yoğunluk fonksiyonu şu şekilde bir gamma fonksiyonu ile ifade edilebilir:
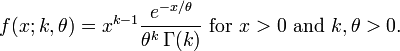
Bu çesit parametrelerle ifade edilme yukarıda verilen bilgi kutusunda ve grafiklerde kullanılmıştır.
Alternatif bir şekilde, gamma dağılımının olasılık yoğunluk fonksiyonu bir şekil parametresi α = k ile ölcek parametresinin tersi olan oran parametresi β = 1 / θ kullanılarak şöyle elde edilir:

Eger α bir pozitif tamsayı ise, o halde
Γ(α) = (α − 1)!
Olasılık yoğunluk fonksiyonu her iki şekli de istatistikçiler tarafından yaygın olarak kullanılmaktadır.
Yığmalı dağılım fonksiyonu
Yığmalı dağılım fonksiyonu bir tanzim edilmiş gamma fonksiyonudur ve bir tamamlanmamış gamma fonksiyonu şeklinde şöyle ifade edilir:

Özellikler
Toplama
Eğer i = 1, 2, ..., N için rassal değişken Xiin dağılımı bir Γ(αi, β) olursa; o halde

Ancak bütün Γ(αi, β) istatistiksel bağımsız olması gerekir.
Gamma dağılımı sonsuz bölünebilirlik özelliği gösterir.
Ölçekleme
Herhangi bir t için tX bir Γ(k, tθ) dağılımı goösterir; bu ifade θnın bir ölçek parametresi olduğunu gösterir.
Üstel ailesi
Gamma dağılımı iki-parametreli üstel ailesinin bir üyesidir ve doğal parametreler değerleri k − 1 ve − 1 / θ; ve doğal istatistikleri X ve ln(X) olur.
Enformasyon entropisi
Enformasyon entropisi şöyle verilir:

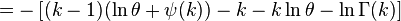

burada ψ(k) bir digama fonksiyonu olur.
KullbackLeibler ayrılımı
'Gerçek' dağılım olan Γ(α0, β0) ile yaklaşık fonksiyon olan Γ(α, β) arasındaki yönlendirilmiş Kullback-Leibler ayrılması şu fonksiyonla verilir:

Laplace dönüşümü
Gamma dağılımının Laplace dönüşümü şudur:

Parametre tahmini
Maksimum olabilirlilik tahmini
Birbirlerinden bagimsiz ve ayni dagilim gosteren N sayida gozlem , ,


Bundan bir log-olabilirlilik fonksiyonu turetilebiliriz:

Bunun θ'ya gore maksimim degerini bulmak icin bu log-olabilirlilik fonksiyonunun birinci turevini alip sifira esitlersek, θ parametresi icin maksimum-olabilirlilik kestirimini buluruz:
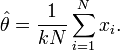
BUnu tekrara log-degisebilirlilik fonksiyonuna koyarsak, elde edilen ifade su olur:

Bunu k'ye gore maksimumunu bulmak icin birinci turevini aliriz ve bunu sifira esitleriz. Sonus sudur:

Burada
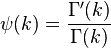
olup bir digamam fonksiyonudur.
k icin kapali-sekilli bir cozum bulunmamaktadir. Bu fonksiyon numerik olarak, hesaplamaya uygun davranis gosterir ve bunun icin bir numerik cozum istenirse, ornegin numerik Newton Yontemi, sonuclar yeterli dakik olur. Bu numerik cozumler icin ilk deger ya "momentler metodu" kullanilarak bulunur ya da su yaklasim kullanilabilir:

Eger su ifadeyi kullanirsak

k yaklasik su degerdedir:

Bu genellikle gercek degerden +/- %1,5 hatali olabilecegi bulunmustur. Bu ilk tahminin Newton-Raphson yontemi icin iyilestirilmesi Choi ve Wette (1969) soyle verilmistir:
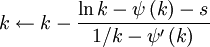
burada

Digamma ve trigamma fonksiyonlarini cok dakiklikle hesaplamak guc olabilir. Fakat, su verilen yaklasim formulleri kullanarak birkaca onemli ondalikli sayiya kadar iyi yaklasim sayilarai bulmak imkani vardir:

ve

Ayrintilar icin bakiniz Choi ve Wette (1969).
Bayes tipi minimum ortalama-kareli hata
Bilinen degerde k ve bilinmeyen degerde 'θ, icin theta icin sonrasal olasilik yogunluk fonksiyonu (θ icin standard olcek-degeistilmez oncel kullanarak) su elde edilir:

Su ifade verilsin

Bunun θ entegrasyonu degiskenlerin degistirilmesi yontemi kullanilarak mumkun olur. Bunun sonucunda 1/θ ifadesinin

parametreleri olan bir gamma dagilimi gosterdigi ortaya cikartilir.
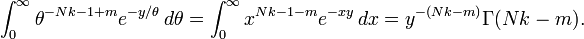
Momentler (m ile m = 0) orantisi alinarak hesaplanabilir:
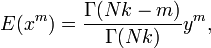
Buna gore theta'nin sonsal dagiligiminin ortalama +/- standart sapma kestiriminin soyle olur:

Gamma dağılım gösteren rassal değişken üretimi
İlişkili dağılımlar
Özel dağılımlar
