-
- Üyelik Tarihi
- 3 Nis 2008
-
- Mesajlar
- 2,499
-
- MFC Puanı
- 0
Gama Fonksiyonu Nedir - Gama Fonksiyonu Hakkında - Gama Fonksiyonları
Gama fonksiyonu Matematikte faktöriyel fonksiyonunun karmaşık sayılar ve tam sayı olmayan reel sayılar için genellenmesi olan bir fonksiyondur. Г simgesiyle gösterilir.

Kompleks düzlemde Analitik devamlılık için n negatif tamsayı olmamalıdır,pozitif tamsayı olmalıdır.

Alıştırma
Öncelikle
(n + 1)n! = (n + 1)! eşitliğini ele alalım,n = 0'alırsak
1.1! = 0! = 1 olur.
aynı işlem kesirli sayılarla yapılabilirmi? diye bir soru akla gelir.
n = 1 / 2 alırsak;
(3 / 2)(1 / 2)! = (3 / 2)!,olması gerekir.Yani
(3 / 2)(1 / 2)! = (3 / 2)!→(3 / 2)! / (1 / 2)! = 3 / 2'olmalıdır
Γ(n) = (n − 1)!' olduğundan;
Γ(5 / 2)→(3 / 2)! 'ye karşılık gelmelidir(eşittir demiyoruz) ve yine
Γ(3 / 2)→(1 / 2)! işlemine karşılık gelmelidir.

Γ(5 / 2) / Γ(3 / 2) = 3 / 2
Buda
Γ(5 / 2) / Γ(3 / 2) = 3 / 2→(3 / 2)! / (1 / 2)! = 3 / 2 varsayımımızı doğruluyor.Denenirse diğer sayılar içinde bunun doğruluğu görülebilir.
Tanım
Ana Tanı
Bu çift Γ(z) gösterim Legendre tarafından yapılmıştır.kompleks sayı z'nin gerçel kısmı (Re[z] > 0) şeklindedir. integral'i

Burada kısmi integrasyon kullanarak, mutlak yakınsaklık gösterilebilir.
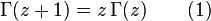
n ! = n · (n − 1) ! faktoriyel fonksiyonunun genel kimliği/tanımı Bu fonksiyonel denklemdir.

Bu iki sonuç bize faktöriyel fonksiyonun gama fonksiyonun özel bir durumu olduğunu gösteriyor. Bütün n Doğal sayılar'ı için .

Γ(z) genellemesi analitik devamlılık için gereklidir.z böylece 0 ve negatif değerler hariç bütün kompleks sayıları meromorfik fonksiyon olarak tanımlar., ( z. = −nbasit kutbu ile rezidü (−1) n/n !).
Alternatif tanımlamalar
0 ve negatif tamsayılar dışında bütün kompleks sayılar z için tanım sonsuz sayıda Gama fonksiyonu için, sırasıyla Euler ve Weierstrass çifti tarafından
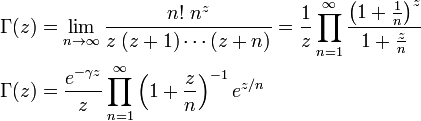
burada γ, Euler-Mascheroni sabiti'dir.
yukarıdaki z nin 0,-1,-2,-3..dışındaki değerleri için Euler tanımı fonksiyonel denklemi basitleştirilmiş şekli,

değişik bir gösterim...
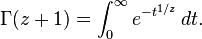
Bazen Gamma fonksiyonu'nun parametrik şekli Laguerre polinomları'nın terimleri içinde verilir;
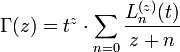 yakınsaklık için
yakınsaklık için
 olmalıdır.
olmalıdır.

Mutlak değer

Gerçel kısım

Hayali kısım
Özel değerler

Gama fonksiyonu Matematikte faktöriyel fonksiyonunun karmaşık sayılar ve tam sayı olmayan reel sayılar için genellenmesi olan bir fonksiyondur. Г simgesiyle gösterilir.

Kompleks düzlemde Analitik devamlılık için n negatif tamsayı olmamalıdır,pozitif tamsayı olmalıdır.

- Reel eksen boyunca gama fonksiyonu
Alıştırma
Öncelikle
(n + 1)n! = (n + 1)! eşitliğini ele alalım,n = 0'alırsak
1.1! = 0! = 1 olur.
aynı işlem kesirli sayılarla yapılabilirmi? diye bir soru akla gelir.
n = 1 / 2 alırsak;
(3 / 2)(1 / 2)! = (3 / 2)!,olması gerekir.Yani
(3 / 2)(1 / 2)! = (3 / 2)!→(3 / 2)! / (1 / 2)! = 3 / 2'olmalıdır
Γ(n) = (n − 1)!' olduğundan;
Γ(5 / 2)→(3 / 2)! 'ye karşılık gelmelidir(eşittir demiyoruz) ve yine
Γ(3 / 2)→(1 / 2)! işlemine karşılık gelmelidir.

Γ(5 / 2) / Γ(3 / 2) = 3 / 2
Buda
Γ(5 / 2) / Γ(3 / 2) = 3 / 2→(3 / 2)! / (1 / 2)! = 3 / 2 varsayımımızı doğruluyor.Denenirse diğer sayılar içinde bunun doğruluğu görülebilir.
Tanım
Ana Tanı
Bu çift Γ(z) gösterim Legendre tarafından yapılmıştır.kompleks sayı z'nin gerçel kısmı (Re[z] > 0) şeklindedir. integral'i

Burada kısmi integrasyon kullanarak, mutlak yakınsaklık gösterilebilir.
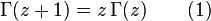
n ! = n · (n − 1) ! faktoriyel fonksiyonunun genel kimliği/tanımı Bu fonksiyonel denklemdir.

Bu iki sonuç bize faktöriyel fonksiyonun gama fonksiyonun özel bir durumu olduğunu gösteriyor. Bütün n Doğal sayılar'ı için .

Γ(z) genellemesi analitik devamlılık için gereklidir.z böylece 0 ve negatif değerler hariç bütün kompleks sayıları meromorfik fonksiyon olarak tanımlar., ( z. = −nbasit kutbu ile rezidü (−1) n/n !).
Alternatif tanımlamalar
0 ve negatif tamsayılar dışında bütün kompleks sayılar z için tanım sonsuz sayıda Gama fonksiyonu için, sırasıyla Euler ve Weierstrass çifti tarafından
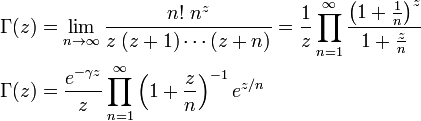
burada γ, Euler-Mascheroni sabiti'dir.
yukarıdaki z nin 0,-1,-2,-3..dışındaki değerleri için Euler tanımı fonksiyonel denklemi basitleştirilmiş şekli,

değişik bir gösterim...
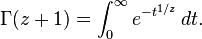
Bazen Gamma fonksiyonu'nun parametrik şekli Laguerre polinomları'nın terimleri içinde verilir;
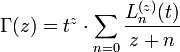


Mutlak değer

Gerçel kısım

Hayali kısım
Özel değerler
