Belirli bir kurala göre art arda gelen sayı dizilerine ardışık sayılar denir.
n bir tamsayı olmak üzere,
Ardışık tamsayılar: 1, 2, 3, 4, n, n + 1, n + 2,
Ardışık çift sayılar: 0, 2, 4, 6, 2n, 2n + 2, 2n + 4,
Ardışık tek sayılar: 1, 3, 5, 7, 2n 1, 2n + 1, 2n + 3,
şeklinde gösterilebilir.
SONUÇ:
=> Ardışık tamsayılar 1 er 1 er artar ve azalır.
=> Ardışık çift ve ardışık tek tamsayılar 2 şer 2 şer artar ve azalır.
ÖRNEK:
a, b, c ardışık doğal sayılardır.
a < b < c
olduğuna göre, 4a + 3b 7c ifadesinin değeri kaçtır?
A) -15
B) -11
C) -7
D) 3
E) 11
ÇÖZÜM:
a = n olsun.
Bu durumda b = n + 1 ve c = n + 2 olur.

Doğru Seçenek: B
Ardışık Sayıların Sonlu Toplamları
n terim sayısı olsun.

ÖRNEK:
1+ 2 + 3 + 4 + ...... + 50 toplamının sonucu kaçtır?
ÇÖZÜM:
1+ 2 + 3 + 4 + ...... + 50 toplamında n = 50 dir.
O halde,
bulunur.
ÖRNEK:
2 + 4 + 6 + ...... + 60 toplamının sonucu kaçtır?
ÇÖZÜM:
2 + 4 + 6 + ...... + 60 toplamında 2n = 60 ve n = 30 dur.
Buna göre, toplam 2 + 4 + 6 + ...... + 60 = 30 .31= 930 elde edilir.
ÖRNEK:
1+ 3 + 5 + ...... + 41 toplamının sonucu kaçtır?
ÇÖZÜM:
1+ 3 + 5 + ...... + 41 toplamında 2n-1 = 41 ve n = 21 dir.
Buna göre, toplam 1+ 3 + 5 + ...... + 41= 212 = 441 elde edilir.
Ardışık Sayı Dizilerinde Terim Sayısı
Ardışık sayı dizilerinde terim sayısını bulmak için ilk terim, son terim ve artış miktarı kullanılır.

NOT:
Sonlu ardışık sayıların toplamını bulmak için aşağıdaki yöntem kullanılır.
r ilk terim, n son terim ve x artış miktarı olsun.
toplamını bulmak için terim sayısı ile ardışık sayı dizisinin ortasındaki terim çarpılır.

ÖRNEK:
5 + 8 +11+ ...... + 77 toplamı kaçtır?
ÇÖZÜM:
Verilen ardışık sayı dizisinde ilk terim 5, son terim 77 ve artış miktarı 3 tür.

ÖRNEK:
Ardışık 5 tamsayının toplamı 95 olduğuna göre, bu sayıların en büyüğü ile en küçüğünün toplamı kaçtır?
ÇÖZÜM:
I. YOL:
Ardışık 5 tamsayının en küçüğüne n diyelim.
Ardışık sayılar 1 er 1 er arttığına göre, sayılar

O halde en küçük sayı n = 17 ve en büyük sayı n + 4 = 21 olur.
Bu sayıların toplamı da 38 dir.
II. YOL:
Verilen 5 sayının toplamı 95 ise 95 terim sayısına yani 5 e bölünürse ortadaki terim elde edilir.
Buna göre, ortadaki yani 3. sayı,
elde edilir.
Dolayısıyla en küçük sayı 19 2 = 17 ve en büyük sayı 19 + 2 =21 bulunur.
Bu sayıların (bilgi yelpazesi.net) toplamı da 38 dir.
ÖRNEK:
Ardışık 11 çift sayının toplamı 1188 olduğuna göre, ortadaki sayı kaçtır?
ÇÖZÜM:
1188 sayısı, 11 e bölünürse ortadaki sayı bulunur.
Buna göre, ortadaki sayı

bulunur.
ÖRNEK:
a, b, c ardışık tamsayılar ve a<b<c olmak üzere,

işleminin sonucu aşağıdakilerden hangisi olabilir?
A) b
B) 2a
C) b+2
D) 2b
E) a+2
ÇÖZÜM:

Doğru Seçenek: D
ÖRNEK:
n bir doğal sayı olmak üzere, 1 den n ye kadar olan doğal sayıların toplamı x ve 12 den n ye kadar olan doğal sayıların toplamı y dir.
x + y = 234 olduğuna göre, x kaçtır?
A) 140
B) 145
C) 150
D) 155
E) 160
ÇÖZÜM:
Doğru Seçenek: C
ÖRNEK:
n bir tamsayı olmak üzere, 3n 4 ile n + 6 sayıları ardışık iki çift tamsayı olduğuna göre, n nin alabileceği değerler toplamı kaçtır?
A) 2
B) 4
C) 8
D) 10
E) 14
ÇÖZÜM:
Sayılar ardışık iki çift tamsayı olduğuna göre, farkları 2 olur.

Buna göre, n nin alabileceği değerler toplamı 6 + 4 = 10 olur.
Doğru Seçenek: D
n bir tamsayı olmak üzere,
Ardışık tamsayılar: 1, 2, 3, 4, n, n + 1, n + 2,
Ardışık çift sayılar: 0, 2, 4, 6, 2n, 2n + 2, 2n + 4,
Ardışık tek sayılar: 1, 3, 5, 7, 2n 1, 2n + 1, 2n + 3,
şeklinde gösterilebilir.
SONUÇ:
=> Ardışık tamsayılar 1 er 1 er artar ve azalır.
=> Ardışık çift ve ardışık tek tamsayılar 2 şer 2 şer artar ve azalır.
ÖRNEK:
a, b, c ardışık doğal sayılardır.
a < b < c
olduğuna göre, 4a + 3b 7c ifadesinin değeri kaçtır?
A) -15
B) -11
C) -7
D) 3
E) 11
ÇÖZÜM:
a = n olsun.
Bu durumda b = n + 1 ve c = n + 2 olur.

Doğru Seçenek: B
Ardışık Sayıların Sonlu Toplamları
n terim sayısı olsun.

ÖRNEK:
1+ 2 + 3 + 4 + ...... + 50 toplamının sonucu kaçtır?
ÇÖZÜM:
1+ 2 + 3 + 4 + ...... + 50 toplamında n = 50 dir.
O halde,
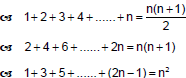
bulunur.
ÖRNEK:
2 + 4 + 6 + ...... + 60 toplamının sonucu kaçtır?
ÇÖZÜM:
2 + 4 + 6 + ...... + 60 toplamında 2n = 60 ve n = 30 dur.
Buna göre, toplam 2 + 4 + 6 + ...... + 60 = 30 .31= 930 elde edilir.
ÖRNEK:
1+ 3 + 5 + ...... + 41 toplamının sonucu kaçtır?
ÇÖZÜM:
1+ 3 + 5 + ...... + 41 toplamında 2n-1 = 41 ve n = 21 dir.
Buna göre, toplam 1+ 3 + 5 + ...... + 41= 212 = 441 elde edilir.
Ardışık Sayı Dizilerinde Terim Sayısı
Ardışık sayı dizilerinde terim sayısını bulmak için ilk terim, son terim ve artış miktarı kullanılır.

NOT:
Sonlu ardışık sayıların toplamını bulmak için aşağıdaki yöntem kullanılır.
r ilk terim, n son terim ve x artış miktarı olsun.
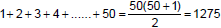
toplamını bulmak için terim sayısı ile ardışık sayı dizisinin ortasındaki terim çarpılır.

ÖRNEK:
5 + 8 +11+ ...... + 77 toplamı kaçtır?
ÇÖZÜM:
Verilen ardışık sayı dizisinde ilk terim 5, son terim 77 ve artış miktarı 3 tür.

ÖRNEK:
Ardışık 5 tamsayının toplamı 95 olduğuna göre, bu sayıların en büyüğü ile en küçüğünün toplamı kaçtır?
ÇÖZÜM:
I. YOL:
Ardışık 5 tamsayının en küçüğüne n diyelim.
Ardışık sayılar 1 er 1 er arttığına göre, sayılar

O halde en küçük sayı n = 17 ve en büyük sayı n + 4 = 21 olur.
Bu sayıların toplamı da 38 dir.
II. YOL:
Verilen 5 sayının toplamı 95 ise 95 terim sayısına yani 5 e bölünürse ortadaki terim elde edilir.
Buna göre, ortadaki yani 3. sayı,
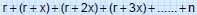
elde edilir.
Dolayısıyla en küçük sayı 19 2 = 17 ve en büyük sayı 19 + 2 =21 bulunur.
Bu sayıların (bilgi yelpazesi.net) toplamı da 38 dir.
ÖRNEK:
Ardışık 11 çift sayının toplamı 1188 olduğuna göre, ortadaki sayı kaçtır?
ÇÖZÜM:
1188 sayısı, 11 e bölünürse ortadaki sayı bulunur.
Buna göre, ortadaki sayı

bulunur.
ÖRNEK:
a, b, c ardışık tamsayılar ve a<b<c olmak üzere,

işleminin sonucu aşağıdakilerden hangisi olabilir?
A) b
B) 2a
C) b+2
D) 2b
E) a+2
ÇÖZÜM:

Doğru Seçenek: D
ÖRNEK:
n bir doğal sayı olmak üzere, 1 den n ye kadar olan doğal sayıların toplamı x ve 12 den n ye kadar olan doğal sayıların toplamı y dir.
x + y = 234 olduğuna göre, x kaçtır?
A) 140
B) 145
C) 150
D) 155
E) 160
ÇÖZÜM:
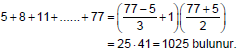
Doğru Seçenek: C
ÖRNEK:
n bir tamsayı olmak üzere, 3n 4 ile n + 6 sayıları ardışık iki çift tamsayı olduğuna göre, n nin alabileceği değerler toplamı kaçtır?
A) 2
B) 4
C) 8
D) 10
E) 14
ÇÖZÜM:
Sayılar ardışık iki çift tamsayı olduğuna göre, farkları 2 olur.

Buna göre, n nin alabileceği değerler toplamı 6 + 4 = 10 olur.
Doğru Seçenek: D