Altın oran, bir bütünün özel iki parçaya bölünmesidir. Genellikle yunan alfabesinin 21. harfi phi (Fi ) Φ kullanılarak sembolize edilir. Matmatiksel bir denklem biçiminde ise aşağıdaki şekilde gösterilir;

a / b = (a + b) / a = 1.6180339887498948420 …

Pi sayısı (bir dairenin çevresinin çapına oranı) gibi irrasyonel bir sayıdır ve altın oranın rakamları da teorik olarak sonsuza kadar devam eder. Fi genellikle 1.618’e yuvarlanır. Bilindiği kadarıyla bu sayı Eski Mısırlılar ve Antik Yunanlar tarafından keşfedilmiş, mimaride, sanatta ve bilimde bir çok kez kullanılmıştır. Altın Oran tarih boyunca Altın kesit, Altın bölüm, İlahi oran, vb. gibi bir çok farklı isim kullanılmıştır. Özellikle Büyük Piramitler ve Parthenon gibi birçok eski kreatif mimari eserde görülebilir. Büyük Piramit Giza’nın tabanın her iki tarafının uzunluğu 756 fit, yüksekliği ise 481 fittir. Tabanın yüksekliğine oranı Altın orana yakın, kabaca 1.5717’dir.

Phidias
Phidias (M.Ö. 500, M.Ö. 432), Parthenon için yaptığı heykellerin tasarımlarında Altın Oranı ilk kez uygulamış olduğu düşünülen Yunan heykeltıraş ve matematikçidir. Platon (M.Ö. 428, M.Ö. 347), Altın Oran’ı matematiksel ilişkilerin evrensel bağlayıcısı olarak kabul etmiştir. Daha sonra, Öklid (M.Ö. 365), Altın Oranı kullanarak bir pentagram oluşturmuştur. Ayrıca “Elementler” adlı kitabında, bir doğruyu 1.618’inci noktasından bölmekten bahsetmiş ve bunu, bir doğruyu ekstrem ve önemli oranda bölmek diye adlandırmıştır.

Leonardo Fibonacci

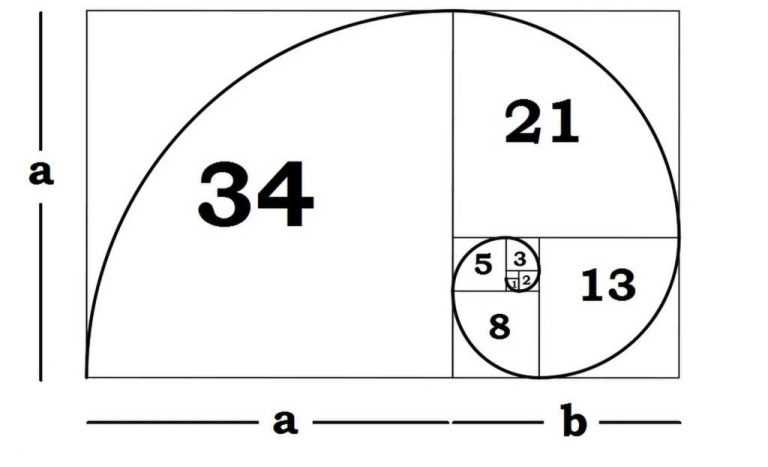
1200 lü yıllarda, İtalyan matematikçi Leonardo Fibonacci; kendi adıyla anılan sayı serisi, Fibonacci dizisinin benzersiz özelliklerinden biri olan Altın oranla doğrudan bağlantılı olduğunu keşfetmiştir. İki ardışık Fibonacci sayı ele alındığında, oranları Altın orana çok yakındır. Rakamlar yükseldikçe, oran 1.618’e daha da yakınlaşmaktadır. Fibonacci dizisinde birbirini izleyen sayılardan 3’ün 5’e oranı 1.666′ dır. 13 ile 21 arasındaki oran 1.615 iken sayı yükseldikçe altın orana daha da yaklaşımlaktadır. Örneğin 144’ün 233’e oranı 1.618 dir.

Altın oran bir dikdörtgene uygulandığında, bu diktörtgene Altın Dikdörtgen adı verilir. Sanatta Altın oranının görünüşü, tüm geometrik formların arasında görsel olarak sanat eserinin, en tatmin edici özelliklerinden biri olarak bilinmektedir. Altın dikdörtgen Altın spiral ile dorudan bağlantılıdır. Fibonacci ölçüleri ile oluşturulan karelerin bitişik olarak dizilmesi ile Altın Spiral elde edilmektedir.

1509’da Luca Pacioli, “İlahi Oran” olarak belirttiği sayıyla ilgili bir kitap yazdı. Daha sonra Leonardo da Vinci eserlerinde fi’den yararlanmış ve Sectio aurea ya da Golden Section olarak adlandırmıştır. Altın oran, Rönesans’ın bir çok resim ve heykellerinde denge ve güzellik elde etmek için kullanıldı. Da Vinci, Son Akşam Yemeği tablosunda, masanın boyutlarında ve duvarların ölçülerinde ve arka planda yer alan ögelerde Altın oranı kullandı. Altın oran Da Vinci’nin Vitruvian Man ve Mona Lisa adlı eserlerinde de görülmektedir. Altın oranını kullanan diğer ünlü sanatçılar arasında Michelangelo, Raphael, Rembrandt, Seurat, Le Corbusier ve Salvador Dali yer alıyor.

Güneş etrafındaki gezegenlerin yörüngelerinin eliptik yapısını keşfeden Johannes Kepler (1571-1630), Altın Oran için: “Geometrinin iki büyük hazinesi vardır; biri Pythagoras’ın teoremi, diğeri ise bir doğrunun Altın Oran’a göre bölünmesidir.”

Mark Barr
Fi yani Φ sembolü, 1900’lü yıllarda Amerikan matematikçi Mark Barr tarafından ilk defa kullanılmıştır. Fi, matematikte ve fizikte görünmeye devam etti. 1970’lerde Roger Penrose, o güne kadar imkânsız olduğu düşünülen, “Penrose Tiles : Yüzeylerin beşli simetri ile katlanması”nı Altın Oran sayesinde başarmıştır. 1980’lerde, Fi, o zaman yeni keşfedilen bir madde biçimi olan, (quasi crystals) yarı kristallerde göründü.

Fi, Estetik anlayışımızda bile günlük hayatımızın içindedir. Yapılan araştırmalarda, Fi’yi hiç bilmeyen sıradan deneklere, rasgele insan yüzleri gösterildi. Deneklerin çekici olarak nitelendirdikleri kişiler, Yüzleri Altın Orana yakın olanlardı. Altın Oran insanlarda içgüdüsel bir çekim oluşturmuştu.

Doğada Altın Oran
Çiçek yaprakları: Bazı çiçeklerdeki yapraklarının sayısı Fibonacci dizilimini takip eder. Darwinci süreçlerde, her bir yaprağın güneş ışığını mümkün olan en iyi şekilde almasını sağlayacak şekilde yerleştirildiğine inanılıyor.

Tohum kafaları: Çiçek tohumları genellikle merkezden üretilir ve alanı doldurmak için dışa doğru açılırlar. Örneğin ayçiçeği altın orana sahiptir ve bu paterni takip eder.

Çam kozalakları: Tohum kabuklarının sarmal biçimi, zıt yönlerde yukarı doğru çıkar haldedir. Spirallerin aldığı adım sayısı Fibonacci sayılarına uyma eğilimindedir.

Ağaç dalları: Ağaç dallarının oluşumu veya bölünmesi Fibonacci dizisinin bir örneğidir. Kök sistemleri ve algler bu oluşum modelini göstermektedir.

Kabuklar: Salyangoz kabukları gibi birçok kabuk Altın spiral için mükemmel örneklerdir.

Spiral Galaksiler: Samanyolu’nun her biri 12 derecelik bir logaritmik spiral olan bir dizi spiral kolu bulunur. Spiralin şekli Altın spiral ile aynıdır ve Altın dikdörtgen herhangi bir spiral galaksinin üzerine çizilebilir.

Kasırgalar : Kabuklara çok benzer, kasırgalar genellikle Altın spiral görüntüler.

Hayvanlar: Yunus, denizyıldızı, kum doları, deniz kestanesi, karınca ve bal arısı gövdeleri altın orana sahip hayvanlardır.

İnsan Bedeni: İnsan göbeğinden ayak tabanına ve kafanın tepesinden göbek deliğine ölçümü Altın oranı verir. Ancak, canlılar arasında altın oranının tek örnekleri biz değiliz. Parmaklarımızın uzunluğu, her bölümü, öncekinden yaklaşık olarak Fi oranında fazladır.

DNA molekülleri: Bir DNA molekülü, çift sarmal spiralin her tam devresinde 34 angstrom’u 21 angstrom ile ölçer. Fibonacci serisinde, 34 ve 21 ardışık sayılardır.