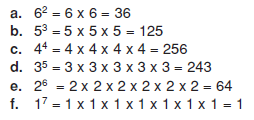6.Sınıf Örüntüler Ve İlişkiler Konu Anlatımı
Örüntülerde Kuralı Bulma
Bir örüntüde n harfi örüntüdeki sayıların sırasını veya yerini ifade eden bir semboldür. Örüntüdeki n sayısına örüntünün n. sayısı, genel sayısı veya temsilci sayı sı denir. n harfine değişken de denir. Örüntülerin ilişkileri değişik biçimlerde bulunabilir ve farklı gösterimlerle ifade edilebilir. Bu ilişkiler tek işlem içeren n + 2, 2n + 8 gibi cebirsel ifadelerdir.
Örnek Soru
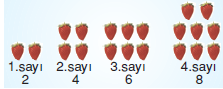
Yukarıda verilen örüntünün kuralını bulalım.
Çözüm
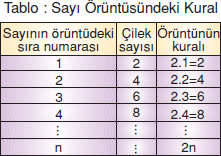
Verilen örüntüde her sayı bir önceki sayıdan 2 fazladır. Sayı örüntülerinde sayılar arasındaki fark eşit olduğundan genel formülde nnin katsayısının 2 olduğuna dikkat edelim.
Örnek Soru
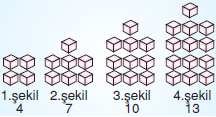
Yukarıda verilen örüntünün kuralını bulalım.
Çözüm
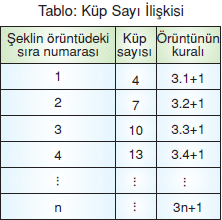
Verilen örüntüde her şekildeki küp sayısı bir önceki şekildeki küp sayısından 3 fazladır. Örüntünün kuralı 3n + 1dir. Örüntünün kuralından yerine yazacağımız sayı bize örüntüdeki şekillerin küp sayısını verir.
Örneğin bu örüntünün 9. şeklindeki küpsayısı: 3.9 + 1 = 27 + 1 = 28dir.
Örneğin bu örüntünün 14. şeklindeki küp sayısı: 3.14+1 = 42+1 = 43tür.
Doğal Sayıların Kendisiyle Tekrarlı Çarpımı
a, b ve n do¤al sayı olmak üzere,
an = b
üslü niceliğinde aya taban, nye üs veya kuvvet, bye değer denir.
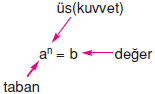
n sayısı anın yanyana kaç defa çarpıldığını belirtir.

Örnek Soru
Aşağıda verilen üslü ifadelerin değerlerini bulalım.

Çözüm
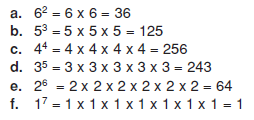
Örüntülerde Kuralı Bulma
Bir örüntüde n harfi örüntüdeki sayıların sırasını veya yerini ifade eden bir semboldür. Örüntüdeki n sayısına örüntünün n. sayısı, genel sayısı veya temsilci sayı sı denir. n harfine değişken de denir. Örüntülerin ilişkileri değişik biçimlerde bulunabilir ve farklı gösterimlerle ifade edilebilir. Bu ilişkiler tek işlem içeren n + 2, 2n + 8 gibi cebirsel ifadelerdir.
Örnek Soru
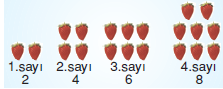
Yukarıda verilen örüntünün kuralını bulalım.
Çözüm

Verilen örüntüde her sayı bir önceki sayıdan 2 fazladır. Sayı örüntülerinde sayılar arasındaki fark eşit olduğundan genel formülde nnin katsayısının 2 olduğuna dikkat edelim.
Örnek Soru

Yukarıda verilen örüntünün kuralını bulalım.
Çözüm

Verilen örüntüde her şekildeki küp sayısı bir önceki şekildeki küp sayısından 3 fazladır. Örüntünün kuralı 3n + 1dir. Örüntünün kuralından yerine yazacağımız sayı bize örüntüdeki şekillerin küp sayısını verir.
Örneğin bu örüntünün 9. şeklindeki küpsayısı: 3.9 + 1 = 27 + 1 = 28dir.
Örneğin bu örüntünün 14. şeklindeki küp sayısı: 3.14+1 = 42+1 = 43tür.
Doğal Sayıların Kendisiyle Tekrarlı Çarpımı
a, b ve n do¤al sayı olmak üzere,
an = b
üslü niceliğinde aya taban, nye üs veya kuvvet, bye değer denir.

n sayısı anın yanyana kaç defa çarpıldığını belirtir.

Örnek Soru
Aşağıda verilen üslü ifadelerin değerlerini bulalım.

Çözüm